darkblue blog

Threading in python and calling out to PostGIS in each thread can work well. Here is an example of using python’s Queue and threading.Thread to break up a large spatial workload into pieces. It turns out that many spatial data problems are naturally parallelizable, and this is one of them.

Per the PostGIS manual, subtraction of one geometry from another, ST_Difference( geomA, geomB) might be described as

GeometryA - ST_Intersection(A,B)

A table of geometries can be processed easily if either geomA or geomB is a constant. But what if there are many thousands of geomA, and hundreds of thousands of geomB? Our example is land type classifications (geomA) and California county land parcels (geomB).

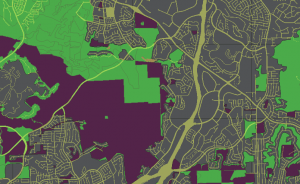
Here is a look at a finished result:

Areas that are colored either green, dark red or gray, are the sum of the area of parcel property in this county, classified into three categories (greenfield, constrained, urban). The remaining yellowish are largely right-of-way (roads, paths, freeways etc). The analysis is done by bringing together two very large input tables – a land classification of the county divided into three classes (14,000 polygons in this example), and the set of parcel properties (~800,000 records).

Start by subtracting all parcels p that touch a given classification polygon l as inner diff

INSERT into landtypes_minus_parcels
SELECT
      l.id_lt,
      l.landtype as landtype_seamless_orig,
      l.other_class,
      CASE when
        st_difference(  l.wkb_geometry,
               st_union(p.wkb_geometry)  )
        is null then l.wkb_geometry
      else
        st_difference(  l.wkb_geometry,
               st_union(p.wkb_geometry)  )
      end
       as tgeom
FROM
   %s l
   inner join
   %s p
   on st_intersects(l.wkb_geometry, p.wkb_geometry)
WHERE l.id_lt = %s
GROUP BY l.id_lt, l.wkb_geometry;

Get a list of primary keys in python from the classification table l

tSQL = '''
select id_lt from %s order by id_lt;
''' % (targ_landtypes)

try:
    gCurs.execute( tSQL )
    gDB.commit()
except Exception, E:
    print str(E)
    raise

idsA  = []
idsTA = gCurs.fetchall()
for tElem in idsTA: idsA.append( tElem[0] )

A psycopg2 query cursor returns an array of tuple – for convenience take the one and only one result per tuple and build a simple list from them. In this analysis, we take the length of the list of primary keys of classification polygons, divide by the desired number of threads, to get a number of classification polygons that will be handled per thread. Since we have an ordered list of primary keys, it is straightforward to pick two keys at a time – upper and lower pkey – and pass them into each thread as dictionary arguments.

tBaseDiv = len( idsA ) / gThreadCount
tBaseOffset = 0
for i in range( gThreadCount ):
    if i == gThreadCount - 1:
       ## last bucket gets any remainder, too
       tEndInd = len( idsA ) - 1
    else:
       tEndInd = tBaseOffset + tBaseDiv - 1

    tD = {
      'start_id': idsA[ tBaseOffset ],
      'end_id': idsA[ tEndInd ]
    }

    tBaseOffset += tBaseDiv
    queue.put( tD )

Next, a unit of work has to be described; a threading.Thread subclass could be defined as follows: upon running, retrieve a parameter Dict from the threads queue, and from it the upper and lower primary key bounds for this thread; for each primary key in this range, execute the inner diff query; when completed, commit() to the database and signal that this thread is complete.

class Thread_ComputeCTWUnit(threading.Thread):
    """Threaded Unit of work"""
    def __init__(self, queue):
      threading.Thread.__init__(self)
      self.queue = queue

    def run(self):
      while True:
        #grabs host from queue
        jobD = self.queue.get()

        tQueuedJobStr = '''
  select id_lt from %s where id_lt >= %s and id_lt < = %s
''' % ( targ_landtypes, jobD['start_id'], jobD['end_id'] )

        #tTmpAnswer = tLocalCurs.fetchone()[0]
        #print 'start_id=',jobD['start_id'],'; end_id=',jobD['end_id'],'; count=',str(tTmpAnswer)

        ##---------------------------
        ## each thread has its own pyscopg2 connection
        try:
          tLocalConn = psycopg2.connect( gDSN )
        except Exception, E:
          print str(E),' start_id=',jobD['start_id']
          self.queue.task_done()
          return

        tLocalCurs = tLocalConn.cursor()
        try:
          tLocalCurs.execute( tQueuedJobStr )
        except Exception, E:
          print str(E)

        tTA_local = tLocalCurs.fetchall()
        for tInd in tTA_local:
            try:
                tLocalCurs.execute( tSQL_primediff % (targ_landtypes,src_parcels,tInd[0]) )
                #tLocalConn.commit()
            except Exception, E:
                print str(E)
                raise

        tLocalConn.commit()
        tLocalConn.close()
        ##---------------------------
        #signals to queue job is done
        self.queue.task_done()
        return

Given 14,000 classified polygons as input, parcel records for a county, running on a 16 core linux machine, and creating 14 threads, each thread will run 1000 queries then commit() back to the database. The runtime in practice is about 15%-30% of the time it would take without threading. One reason for this is that even though each thread has the same number of classification polygons to work on, not all polygon subtractions are created equal, so inevitably some sets of queries take longer than others.