Recently the task of combining and tiling some large GeoTIFFs came up.. so began an investigation of adding threading support to gdal_retile.py
Unfortunately, it is widely known that python is not the best environment for multithreaded work, due to the global interpreter lock (GIL). However, while building threading support for some routine postgis tasks recently, I had quickly found that dispatching a series of computationally intensive PostGIS tasks via psycopg2 in python threading can work quite well. In that case the bulk of the work is done by a large, external engine (PostGIS) and python just acts as a brain to the brawn. I started on this gdal_retile.py experiment with an idea that CPU intensive parts of a gdal_retile.py job, perhaps color-space conversion and JPEG compression, might tip a balance such that the python threading itself was no longer a bottleneck.
I wanted to find a straightforward threading pattern in python that was suitable for breaking up gdal_retile.py’s inner loops.
A Threading Pattern in Python
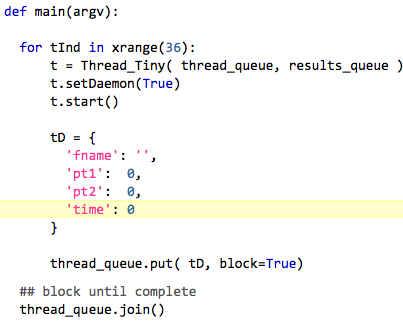 After some experimentation, this program worked well enough.
After some experimentation, this program worked well enough.
- Thread_Tiny is a threading.Thread subclass, whose
__init__ function takes two Queue objects as arguments.
- thread_queue maintains the threads themselves
- results_queue where each thread pushes its result before being disposed
- tD a dict containing anything the main program wants to pass to a new Thread
- put() an args dict into thread_queue. A live thread will pick it up. If all threads are busy working, wait internally until a slot becomes available before adding the queue element
- app waits for all threads to complete
This construct seemed sufficiently complete to be a template for breaking up a moderately complex utility like gdal_retile.py
Reworking gdal_retile.py
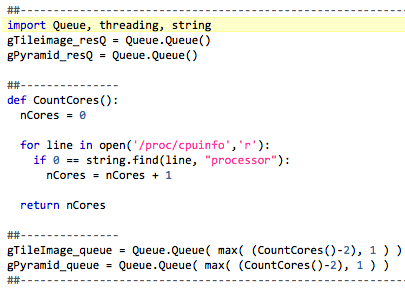 I found that there were really two places that an inner loop repetition was being done. Once where the input was being split into tiles as
I found that there were really two places that an inner loop repetition was being done. Once where the input was being split into tiles as TileResult_0, and secondly when building a plane of a pyramid TileResult_N. (in gdal_retile.py either operation can be omitted)
Solution: A utility function Count_Cores() returns the number of cores in the Linux operating environment. Define a thread_queue and result_queue – each instances of Queue.Queue – for each case. A difference is that a thread_queue is created such that there is only one slot per desired active process. This way the thread_queue runs Threads in an orderly way. The number of active Threads is limited to “cores minus two” or one by limiting the number of slots available in a new thread_queue. Instead of possibly clogging execution with an arbitrarily large set of new Threads to execute at initialization time, only N threads can run at any given time.
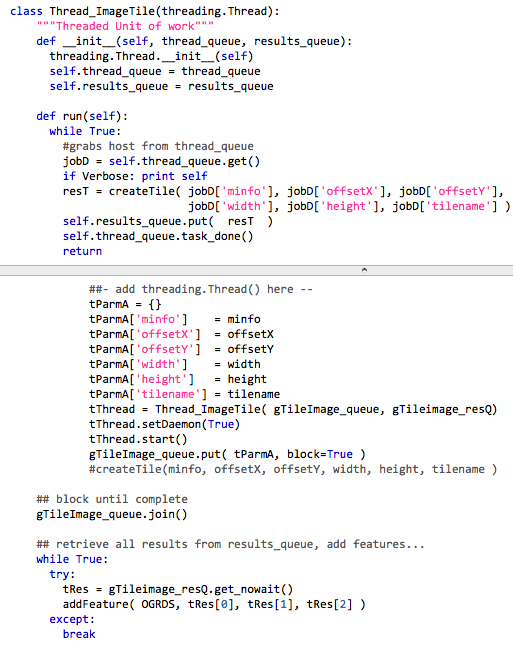
Next, a basic unit of work has to be defined that can be turned over to Threads. In tileImage() there is a call to createTile(), which takes as arguments: a local object called mosaic_info; offsets X,Y; height and width; a tilename; and an object representing an OGR Datasource. That datasource is open and has state, and therefore is not shareable. However I discovered that inside createTile() the only thing the OGR datasource is used for is a single, write-only append of a feature describing the output tile’s BBOX and filename. What if a result_queue replaced the non-shareable datasource passed into createTile() and each thread simply pushes its result into the result_queue ? When all threads have completed, iterate and retrieve each thread result, adding each to the OGRDS data source as a feature. Here is some code…
A Second Comparison
Fortunately, while discussing this on #gdal Robert Coup (rcoup) happened to be online. In his organization there was another attempt at making gdal_retile.py parallel too, but the results were not satisfying. rcoup tossed the code over, and I ran that as well.
Some Results?
time gdal_retile.py -s_srs EPSG:900913 -co "TILED=YES" -co "COMPRESS=JPEG" -ps 1024 1024 -r "bilinear" -co PHOTOMETRIC=YCBCR -targetDir out_dir_stock Fresno_city_900913.tif
In the end, the version rcoup sent, the threaded version described here, and the stock version, all ran against a 77,000 pixel x 84,000 pixel GeoTIFF (18G, three bands) in about the same 50 minutes each on a local machine (producing a matching 6309 tiles). I suspect that something in the GDAL python interfaces (aside from the GIL) is preventing real parallelism from kicking in, though there are a lot of corners for problems to hide in just this small example.
Long ago, hobu had this to say



 After some experimentation, this program worked well enough.
After some experimentation, this program worked well enough. I found that there were really two places that an inner loop repetition was being done. Once where the input was being split into tiles as
I found that there were really two places that an inner loop repetition was being done. Once where the input was being split into tiles as 